Harmonic Resonance Theory: An Alternative to the "Neuron Doctrine" Paradigm of Neurocomputation to Address Gestalt properties of perception

2 The Neuron Doctrine

Ever since Ramon y Cajal demonstrated that the nervous system is composed of discrete cells rather than a continuous network, the neuron doctrine (Barlow 1972, 1995, Shepard 1991) has emerged as the dominant paradigm of neurocomputation. The rapid propagation of ions through the intracellular fluid, in combination with the relatively slow transmission across the chemical synapse suggest that the neuron behaves as a quasi-independent processor that responds to the input signals received through its dendrites to produce an output signal through the axon and its collaterals. Hodgkin & Huxley (1939) demonstrated that the frequency of action potentials correlates with the input applied to the cell presynaptically. This in turn suggests a rate code, in which the significant signal is not carried by the individual action potentials, as had been previously assumed, but by the frequency of their occurrence.

2.1 Feature Detector Hierarchy

Neuroscience experienced something of a revolution with the discovery by Hubel and Wiesel of cells in the visual cortex that respond to particular features presented at specific locations in the visual field. Some cells were found to respond to simple features such as a local edge of a particular location and orientation, while other cells had more complex response functions, as if in response to spatial combinations of simple cell responses. Eventually whole hierarchies of cells were identified in various regions of the visual cortex, with cells in the higher cortical areas responding to ever more complex combinations of lower level primitives. This data suggests that the cortex has a hierarchical organization that encodes the presence of particular patterns in the visual field by the activation of lower and higher order cells tuned specifically to those patterns.

The computational principle behind these cortical feature detector cells has also been proposed. Hubel (1988) suggests that lower level feature detectors are triggered by visual edges by the same essential principle as that used in edge detectors employed in computer image processing, i.e. each cell is equipped with a receptive field whose spatial pattern of excitatory and inhibitory synapses match the spatial feature that the cell is tuned to detect. In essence these lower level feature detectors perform a local template match to the pattern of activation detected in their input field, with the pattern of synapses in the dendritic field acting as the spatial template. Higher order cells respond to more complex combinations of lower level features by being connected to the corresponding lower order feature cells by way of the appropriate pattern of excitatory and inhibitory connections.

At the highest levels of the cortex information is presumed to be encoded by a massively interconnected network of cells, each cell representing a complex combination of lower level featural primitives (Barlow 1972). The higher cortical neurons each represent some aspect of the complex perceptual and cognitive experience, and conversely, any particular experience is represented by a characteristic constellation of innumerable activations of higher cortical neurons.

2.2 Abstraction and Compression

One essential aspect of this paradigm of representation is that extended elements of perceptual experience, such as the perception of whole objects in a scene, are encoded in a compressed manner in higher cortical centers by the activation of a single cell or small set of cells dedicated individually or collectively to the representation of those objects. The number of cells required to encode that object at the higher level therefore is much smaller than the number of lower level cells that encode the object's component features. In other words information is progressively reduced or abstracted as it progresses up through the cortical hierarchy, from the more explicit primary areas to the more abstract association areas. There is a sequential progression implied in this paradigm of representation, with information flowing bottom-up from primary to higher areas, although reciprocal feedback pathways implicate some kind of top-down process, presumably for the purposes of cognitive expectation and perceptual completion.

2.3 Fragmented Architecture

Another essential aspect of the neuron doctrine is its fragmentary or distributed nature. For although the primary cortical areas reveal topographical maps of the sensory world, as in the primary visual and somatosensory cortices, higher cortical areas are fragmented into multiple cortical maps of those same sensory areas, as in the secondary visual and somatosensory areas. Each of these multiple copies of the same sensory field appears to be specialized for the representation of particular aspects or modalities of that sensory experience, such as color, shape, motion, and binocular disparity. Even within each of these maps, the features are represented in fragmentary form, with separate cells dedicated to encoding features of different orientations, shape, binocular disparities, color, directions of motion, etc. at every location within that visual map. This is suggestive of an analytical representational strategy in which the sensory world is broken down into its component features, each of which is represented by distinct cortical mechanisms tuned to detect those features.

The neuron doctrine is by no means universally accepted in neuroscience. Alternative paradigms have been proposed, such as Köhler & Held's electric field theory (Köhler & Held 1947), Pribram's holographic theory (Barrett 1969, Pribram et al. 1974, Pribram 1999), De Valois & De Valois' theory of Fourier coding (De Valois & De Valois 1979, 1988), von der Malsburg's temporal correlation hypothesis (von der Malsburg & Schneider 1986, von der Malsburg 1987), Penrose's theory of quantum consciousness (Penrose 1989, 1994), Harrison's and Smythies' theory of consciousness in hidden dimensions (Harrison 1989, Smythies & Beloff 1989, Smythies 1994), to name a few. However none of these paradigms has ever been worked out in enough detail to specify exactly how perceptual information is encoded or processed in the brain. By contrast, the neuron doctrine has the distinct merit of being clear and explicitly defined, and therefore amenable to quantitative computer simulations. Therefore in the absence of a more viable alternative, the neuron doctrine remains to this day the dominant paradigm of neurocomputation, and much of the contemporary research, and discussion of the results of that research, is based implicitly or explicitly on the assumptions of this paradigm. The neuron doctrine is also fairly consistent with contemporary understanding of the neuron at the cellular level. However this concept of neurocomputation has some serious shortcomings that come to light when considering a larger systems level of analysis of brain function.

3 Problems with the Neuron Doctrine

In the first place there is a problem with the notion of the visual neuron as a feature detector that operates by way of a hard-wired receptive field of excitatory and inhibitory synapses anchored to the tissue of the brain. For this concept is no different than a template theory, the limitations of which are well known. A template is a spatial map of the pattern to be matched, which is inherently intolerant to any variation in the stimulus pattern. For example a mismatch will be recorded if the pattern is presented at a different location, orientation, or spatial scale than that encoded in the template.

The solution to the problem of invariance commonly proposed in neural modeling is a feature based approach, i.e. to break the pattern into its component features, and detect those local features independently of the whole (Selfridge 1959, Marr 1982, Biederman 1987). Very simple features such as oriented edges, bars, or corners, are sufficiently elemental that it would not be prohibitive to provide templates for them at every location and orientation across the visual field. In the purest form of this concept, the spatial match represented by the single global template is replaced by an enumerative match that tallies the number and type of local features present in some region of the visual field, and matches this list against the list of features characteristic of the global form. For example a square might be defined by the presence of four corners, each of which might be detected by a local corner detector applied at every location throughout a local region of the image. The enumerative listing of four corner features would be the same for squares of different rotations, translations, and scales, and therefore the feature list as a representation is invariant to rotation, translation, and scale.

Despite the current popularity of the feature detector concept in neural network models, the fundamental limitations of this approach to perception were pointed out decades ago by Gestalt theory. In the first place, local features cannot be reliably identified in the absence of the global context. For example a corner detector in computer simulations will typically generate countless corner responses in a natural scene, only a small fraction of which would be identified as legitimate corner features in the global context. Another problem with the feature based approach is that in the tally of detected features, it is impossible to determine reliably which features belong to which objects. Whatever local region is selected for the tally of detected features, might just as well include features from several different objects to confound the feature list, and conversely, the object centered on that region will often extend out beyond the region, and thereby lose critical features from its feature list. A pure feature based system would also be easily misled by spatial occlusions, which occur commonly in visual scenes, but appear to pose no serious problem to visual recognition.

Hybrid solutions have also been proposed in which the object template is defined as a pattern of regions, each of which represents an approximate locus for a particular feature (Selfridge 1959, Biederman 1987). For example a square might be defined as four circular regions around a center, each of which defines the possible range of a corner feature at that point, which would be searched out by corner detectors applied through a range of orientations throughout each of those regions. The positional and orientational tolerance afforded by this scheme allows a multitude of different variations of a square to stimulate the same square template. While the object template is thus rendered somewhat rotation and scale sensitive, the tolerance allowed in its component features permits a smaller number of object templates than would be required in a simple template model to recognize all possible variations of the square.

However the hybrid scheme is also fundamentally flawed, because the feature-based detection of the individual component features suffers the same problems as a pure feature-based scheme, being easily confused by extraneous features in each region of interest, while the template-like detection of the global configuration of those local features suffers all the problems inherent in a template-based scheme, with hard limits to the range of variability of each component feature. A more fundamental problem with this concept is that the range of legitimate locations and orientations for any component feature cannot be defined in the abstract, but only relative to the other features actually present. For example if one corner of a square is detected, the exact location and orientation of that corner constrains the permissible locations of the other three corners much more precisely than would be encoded in the object template. Therefore there are many possible configurations of corners that would register to the hybrid model as a square, only a small fraction of which would correspond to legitimate squares.

The feature based approach to visual recognition can be implemented relatively easily in computer algorithms (Ballard & Brown 1982, Marr 1982). However despite decades of the most intensive research, no algorithm has ever been devised that can perform reliably except in the most controlled visual environments. The problem with both the feature based model and with the hybrid model is that they confuse invariance to stimulus variation with a blindness to those variations. For the hybrid square detector that responds to a square knows little about the exact configuration of the corners of that particular square, and the enumerative feature detector knows even less. This is in contrast to our subjective experience in which the region of the visual field that is recognized as belonging to a square is perceived to as high a resolution as the edges of the square itself, even when those edges are not actually present in the stimulus, like the illusory sides of a Kanizsa figure. Furthermore, we can easily indicate where an occluded or missing corner of a square or triangle ought to be located, based on the configuration of the rest of the figure.

The problems inherent in template and feature based detection apply not only to invariance in the perception of simple objects and their component features, but to the whole concept of a featural hierarchy, extending up to higher order complex objects or concepts. For the principle of invariance implies a many-to-one relation between the many possible stimulus variations that all indicate the one recognized object. What is required is a kind of top-down completion that makes use of the higher level recognition of the object to determine what its expected component parts should be. But this feedback is complicated by the many-to-one relation in the bottom-up direction, because a simplistic top-down feedback from the invariant recognition node would involve a one-to-many relation to activate every possible combination of local feature nodes that can ever trigger that invariant node. If on the other hand the top-down feedback is only directed to feature nodes which have actually detected some feature, this would preclude the perceptual filling-in of features absent from the stimulus, and thereby defeat the whole purpose of the feedback.

4 Adaptive Resonance Theory

Although the idea of visual processing as a feed-forward progression through a hierarchical architecture represents the most direct or simplistic form of the neuron doctrine, there has been a growing awareness of the need for some kind of complementary top-down processing function, both on perceptual grounds to account for expectation and perceptual completion as seen in the Kanizsa figure, and on neurophysiological grounds to account for the reciprocal feedback pathways identified neurophysiologically, running from higher to lower cortical areas. Several theorists have proposed neural network models to greater or lesser degree of computational specificity that incorporate some kind of feedback function (Fukushima 1987, Carpenter & Grossberg 1987, Grossberg & Mingolla 1985, 1987, Damasio 1989). Unfortunately these models have been persistently handicapped by the template-like concept of the neural receptive field inherent in the neuron doctrine, which makes it impossible for them to provide an adequate account of the joint properties of invariance in recognition, and specificity in completion phenomena.

Perhaps the most explicit model of neural feedback is seen in the Adaptive Resonance Theory (ART, Carpenter & Grossberg 1987). The principal focus of ART is on the manner in which a neural network model detects novelty in a stream of input patterns, and uses that information to categorize the input patterns on the basis of novelty. The significant property of this model in the present context is not in the details of its learning mechanism, but in the manner in which bottom-up information is mixed with top-down information stored in the learned synaptic weights, as a model of cognitive expectation or perceptual completion. The significant feature of the ART model is that the pattern recognition nodes in what is called the F2 layer, are equipped not only with bottom-up receptive fields for pattern recognition, but also with projective fields that propagate top-down back to the input or F1 layer, and the pattern of synaptic weights in these projective fields generally match the bottom-up weights used for recognition. If, after learning is complete, a partial or incomplete pattern is presented at the input, that pattern will stimulate the activation of the single F2 node whose synaptic weights best match the input pattern. Top-down feedback from that F2 node will in turn impinge its pattern back on the F1 layer, filling-in or completing even the missing portion of the pattern, in a manner that is suggestive of perceptual completion of missing or occluded portions of a recognized object. The fact that the F2 nodes encode whole categories of similar patterns, rather than exact single patterns, embodies a kind of invariance in the model to the variations between patterns of the same category.

4.1 Problems with Adaptive Resonance

The invariance embodied in the principle of adaptive resonance differs fundamentally from the invariance observed in perception, because the synaptic weights of the F2 node after learning several patterns, encode only a single pattern at a fixed location in the model, and that pattern is a kind of average, or blurring together of all of the patterns that belong to that category. In other words the system would behave much the same if all of the patterns of a particular category were first averaged together and then learned as a single pattern, rather than presented in sequence as variations on a central theme. This imposes a severe restriction on the kind of variation that can be tolerated within a category, for it requires a significant overlap between patterns within a particular category, otherwise the average of the patterns in that category would produce only a featureless blur. As a model of learning and categorization this is not necessarily a fatal problem, as long as the features represented by the F1 nodes are presumed to already be invariant to stimulus variation, i.e. that they encode significant and stable characteristics of the stimulus pattern, and therefore significantly similar patterns would be expected to have considerable overlap in their F1 feature representation. However the principle of adaptive resonance is inadequate as a general model of top-down feedback for perceptual completion across an invariance relation, because the feedback in this model can only complete a single variant of the recognized pattern in a rigid template-like manner, and that pattern is no more than a blurred together average of all of the patterns of that particular category.

Consider by contrast, the property of spatial invariance in visual recognition. A spatial pattern, for example the shape of the letter E, has very little overlap, point for point, with variations of that pattern at different orientations. And yet those rotated patterns are not perceived as approximate or imperfect letter E's with diminished recognition confidence, but each one is perceived as a perfect E shape, although it is also perceived to be rotated by some angle. If on the other hand the pattern is truly incomplete, like the shape of the letter F considered as an incomplete E shape, this does indeed register perceptually as a partial or imperfect match to the shape of the letter E. Furthermore, identification of the F shape as an incomplete E immediately highlights the exact missing segment, i.e. that segment is perceived to be missing from a very specific portion of the figure, and the exact location of that missing segment varies with the location, orientation, and scale of the F stimulus. This is a very different and more powerful kind of invariance and completion than that embodied in the ART model. And yet it is exactly the kind of invariance to stimulus variation that would be required in the F1 node representation to make the ART model at all viable as a model of recognition.

The problem can be traced to the central principle of representation in the model, which is a spatial template that is anchored to the tissue of the brain in the form of a fixed receptive field. This mechanism is therefore hard-wired to recognize only patterns that appear at exactly the same physical location as that template in the brain. The problem of invariance in the ART model becomes abundantly clear when attempting to apply its principle of invariance to the spatial variations of rotation, translation, and scale. Learning rotation invariance in the ART model for a pattern like E would be equivalent to learning the single pattern constructed by the superposition of Es at all orientations simultaneously, which creates nothing but a circular blur. And the model after training would respond more strongly to this circular blur than to any actual letter E. Adding translation and scale invariance to the system would involve learning the superposition of every rotation, translation and scale of the learned pattern across the visual field, which would produce nothing but a uniform blur.

The invariance embodied in the ART model to variations in the patterns within a particular category is not really an invariance, but is more of a blindness to those variations, because when detecting a pattern in the input, the F2 recognition mechanism cannot determine which of the allowable variations of the pattern are actually present on the input. What is required to account for invariance in perception is a system that can detect the characteristic pattern of the input despite stimulus variations, and yet have a capacity to complete a partial pattern with respect to the specific variation of the pattern present on the input field; in other words, invariance in recognition, but specification in completion. The fact that this functionality is in principle beyond the capacity of the neural receptive field was recognized already by Lashley (1942), and was a central theme of Gestalt theory.

5 The Binding Problem

The subjective conscious experience exhibits a unitary and integrated nature that seems fundamentally at odds with the fragmented architecture identified neurophysiologically, an issue which has come to be known as the binding problem. For the objects of perception appear to us not as an assembly of independent features, as might be suggested by a feature based representation, but as an integrated whole, with every component feature appearing in experience in the proper spatial relation to every other feature. This binding occurs across the visual modalities of color, motion, form, and stereoscopic depth, and a similar integration also occurs across the perceptual modalities of vision, hearing, and touch. The question is what kind of neurophysiological explanation could possibly offer a satisfactory account of the phenomenon of binding in perception?

One solution is to propose explicit binding connections, i.e. neurons connected across visual or sensory modalities, whose state of activation encodes the fact that the areas that they connect are currently bound in subjective experience. However this solution merely compounds the problem, for it represents two distinct entities as bound together by adding a third distinct entity. It is a declarative solution, i.e. the binding between elements is supposedly achieved by attaching a label to them that declares that those elements are now bound, instead of actually binding them in some meaningful way.

Von der Malsburg proposes that perceptual binding between cortical neurons is signalled by way of synchronous spiking, the temporal correlation hypothesis (von der Malsburg & Schneider 1986). This concept has found considerable neurophysiological support (Eckhorn et al. 1988, Engel et al. 1990, 1991a, 1991b, Gray et al. 1989, 1990, 1992, Gray & Singer 1989, Stryker 1989). However although these findings are suggestive of some significant computational function in the brain, the temporal correlation hypothesis as proposed, is little different from the binding label solution, the only difference being that the label is defined by a new channel of communication, i.e. by way of synchrony. In information theoretic terms, this is no different than saying that connected neurons posses two separate channels of communication, one to transmit feature detection, and the other to transmit binding information. The fact that one of these channels uses a synchrony code instead of a rate code sheds no light on the essence of the binding problem. Furthermore, as Shadlen & Movshon (1999) observe, the temporal binding hypothesis is not a theory about how binding is computed, but only how binding is signaled, a solution that leaves the most difficult aspect of the problem unresolved.

I propose that the only meaningful solution to the binding problem must involve a real binding, as implied by the metaphorical name. A glue that is supposed to bind two objects together would be most unsatisfactory if it merely labeled the objects as bound. The significant function of glue is to ensure that a force applied to one of the bound objects will automatically act on the other one also, to ensure that the bound objects move together through the world even when one, or both of them are being acted on by forces. In the context of visual perception, this suggests that the perceptual information represented in cortical maps must be coupled to each other with bi-directional functional connections in such a way that perceptual relations detected in one map due to one visual modality will have an immediate effect on the other maps that encode other visual modalities. The one-directional axonal transmission inherent in the concept of the neuron doctrine appears inconsistent with the immediate bi-directional relation required for perceptual binding. Even the feedback pathways between cortical areas are problematic for this function due to the time delay inherent in the concept of spike train integration across the chemical synapse, which would seem to limit the reciprocal coupling between cortical areas to those within a small number of synaptic connections. The time delays across the chemical synapse would seem to preclude the kind of integration apparent in the binding of perception and consciousness across all sensory modalities, which suggests that the entire cortex is functionally coupled to act as a single integrated unit.

6 Atomistic v.s. Holistic Principle of Computation

The neuron doctrine incorporates an atomistic assumption, that neurocomputation involves discrete signals communicated along fixed transmission lines between discrete computational elements. The western scientific tradition has a particular bias in favor of an atomistic view, not only of neurocomputation, but of the principles of computation in general. For the reductionist approach favored by western science involves breaking complex problems into simpler pieces which can then be analyzed individually. That is why the discovery by Cajal of the discrete cellular structure of the nervous system triggered an intensive program of investigation of the properties of the individual neuron, in the hope that this would shed light on the operation of the larger nervous system made up of those elementary units. There are certain classes of physical systems for which this analytical approach works well, specifically, for systems whose component elements operate relatively independently, i.e. when the processes and mechanisms active within the element are more closely coupled than those that operate between elements. However this atomistic view of neuroscience is nothing more than an optimistic assumption, because atomistic systems are incomparably easier to study and to characterize mathematically than are holistic or widely coupled and dynamic feedback systems. But although it would be very convenient for neuroscience if the brain worked on an atomistic principle, Gestalt theory has demonstrated with a great variety of different phenomena that this is in fact not the case, and that the brain operates on a holistic, emergent principle of computation.

Further evidence for holistic processes in the brain comes from electro-encephalogram (EEG) recordings which reveal global electrical oscillations that pervade the entire cortex. This global resonance is now beginning to manifest itself also in neurophysiological recordings in the form of synchronous oscillations. In fact the synchronous spiking of remote cortical neurons is difficult to account for in conventional neural terms, because the phase of the spiking signal should become scrambled as it propagates down the axon collaterals and dendrites of the pre- and post-synaptic cells respectively, due to the random thicknesses and irregular path lengths of those many parallel branches. The synchrony should be further disrupted by the spike train integration across the chemical synapses, each of which acts as a low-pass filter, blurring the sharp spike of the pre-synaptic action potential into a smooth rise and decay in the post-synaptic cell. The fact that a high resolution temporal synchrony is observed across remote cortical areas connected by countless parallel paths through countless synaptic junctures suggests that this synchrony is actually transmitted by some other means. In fact it has been shown (Pribram 1971, Bland et al. 1978) that the discrete spiking of the action potentials is superimposed on a more subtle graded potential oscillation, and Pribram (1971) showed that the graded potential oscillation persists even when the spiking discharge falls below threshold. This suggests that the spiking discharge is not the causal origin of the neural signal, but merely the overt manifestation of a more subtle underlying electrical oscillation, like the white caps on ocean waves, and that oscillation seems to pervade the neural tissue unrestricted by the boundaries of the cell. The whole concept of the neuron doctrine has blinded neurophysiologists to the possibility of significant signals that pervade the extracellular matrix, for it is assumed that signals which are neither channeled by the cell wall, nor gated by the chemical synapse, cannot possibly take part in meaningful computation. The Gestalt perspective on the other hand suggests that it is just that kind of holistic field-like process which must be sought out to account for the most significant and interesting aspects of neurocomputation.

7 Harmonic Resonance Theory

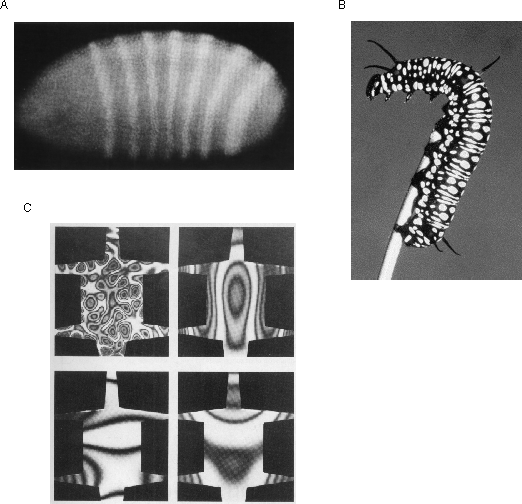
The properties of perception as observed phenomenally and as described by Gestalt theory are truly baffling when it comes to proposing a computational mechanism to account for those properties. However there is one physical phenomenon that exhibits exactly those baffling properties observed in perception, and that is the phenomenon of harmonic resonance, or the representation of spatial structure expressed as patterns of standing waves in a resonating system. This tantalizing similarity cannot be coincidental, considering that no other physical mechanism or phenomenon has ever been identified that exhibits these same enigmatic properties. The most remarkable property of harmonic resonance is the sheer number of different unique patterns that can be obtained in even the simplest resonating system. A pioneering study of more complex standing wave patterns was presented by Chladni (1787) who demonstrated the resonant patterns produced by a vibrating steel plate. The technique introduced by Chladni was to sprinkle sand on top of the plate, and then to set the plate into vibration by bowing with a violin bow. The vibration of the plate causes the sand to dance about randomly except at the nodes of vibration where the sand accumulates, thereby revealing the spatial pattern of nodes. This technique was refined by Waller (1961) using a piece of dry ice pressed against the plate, where the escaping gas due to the sublimation of the ice sets the plate into resonance, resulting in a high pitched squeal as the plate vibrates. Figure 1 (adapted from Waller 1961 P. 69) shows some of the patterns that can be obtained by vibrating a square steel plate clamped at its midpoint. The lines in the figure represent the patterns of nodes obtained by vibration at various harmonic modes of the plate, each node forming the boundary between portions of the plate moving in opposite directions, i.e. during the first half-cycle, alternate segments deflect upwards while neighboring segments deflect downwards, and these motions reverse during the second half-cycle of the oscillation. The different patterns seen in Figure 1 can be obtained by touching the plate at a selected point while bowing at the periphery of the plate, which forms a node of oscillation at the damped location, as well as at the clamped center point of the plate. The plate emits an acoustical tone when bowed in this manner, and each of the patterns shown in figure 1 corresponds to a unique temporal frequency, or musical pitch, the lowest tones being produced by the patterns with fewer large segments shown at the upper-left of figure 1, while higher tones are produced by the higher harmonics depicted towards the lower right in the figure. The higher harmonics represent higher energies of vibration, and are achieved by damping closer to the central clamp point, as well as by more vigorous bowing. There are many more possible patterns in a square plate than those depicted in figure 1, which would be revealed by suspending the plate without clamping, allowing patterns which do not happen to exhibit a node at the center of the square, and of course there are many more patterns possible in plates of different shapes (Waller 1961), and many more still in volumetric resonant systems such as a vibrating cube or sphere, which define three-dimensional subdivisions of the resonating volume, although these have not received much attention due to the difficulty in observing the standing wave patterns within a solid volume or volumetric resonant cavity. Faraday (1831) extended Chladni's phenomenon by observing standing waves on the surface of liquids, which produces geometrical arrays of standing waves on the surface of the fluid in the form of concentric rings, parallel ridges, grid and checkerboard patterns, arrays of cone-like points, and even brick patterns. This work has been extended more recently by Cristiansen et al (1992), Kumar & Bajaj (1995), Kudrolli & Gollub (1996), Kudrolli et al. (1998) and others, who have demonstrated patterns of equilateral triangles, regular hexagons, superlattice, and quasi-crystal array patterns by driving the oscillation of the fluid layer with a controlled waveform. Figure 2 shows some of the patterns produced by Kudrolli et al. It seems that this work is only touching the surface of the full potential of this phenomenon for producing complex geometrical patterns by relatively simple driving oscillations.

Figure 1

Chladni figures for a square steel plate (adapted from Waller 1961) demonstrates the fantastic variety of standing wave patterns that can arise from a simple resonating system. A square steel plate is clamped at its midpoint and sprinkled with sand. It is then set into vibration either by bowing with a violin bow, or by pressing dry ice against it. The resultant standing wave patterns are revealed by the sand, that collects at the nodes of the oscillation where the vibration is minimal.

Figure 2

Various patterns of standing waves on fluid surfaces generated by vibrating the containing vessels with various driving frequencies, producing A: hexagonal, B: rectangular lattice, C: quasi-crystal patterns, among many more. D: This pattern is defined more by the shape of the walls of the container rather than by the driving waveform, showing how interference patterns in the resonating system tend to subdivide the resonating system into periodic and symmetric sub-patterns in an essentially Gestalt manner.

7.1 Reaction-Diffusion Systems

The utility of standing wave patterns as a representation of spatial form is demonstrated by the fact that nature makes use of a resonance representation in another unrelated aspect of biological function, that of embryological morphogenesis, or the development of spatial structure in the embryo. After the initial cell divisions following fertilization, the embryo develops into an ellipsoid of essentially undifferentiated tissue. Then, at some critical point a periodic banded pattern is seen to emerge as revealed by appropriate staining techniques, shown in figure 3 A. This pattern indicates an alternating pattern of concentration of morphogens, i.e. chemicals that permanently mark the underlying tissue for future development. This pattern is sustained despite the fact that the morphogens are free to diffuse through the embryo. The mechanism behind the emergence of this periodic pattern is a chemical harmonic resonance known as reaction diffusion (Turing 1952, Prigogine & Nicolis 1967, Winfree 1974, Welsh et al. 1983) in which a continuous chemical reaction involving a morphogen P catalyzes the production of more morphogen P as well as of a morphogen S, but the concentration of morphogen S in turn inhibits production of morphogen P (see Gilbert 1988 pp 655-661 for a summary). The result of this circular reaction is analogous to the periodic patterns of a resonating steel plate. The chemical harmonic resonance in the embryo can thereby define a spatial addressing scheme that identifies local cells in the embryonic tissue as belonging to one or another part of the global pattern in the embryo by way of the relative concentration of certain morphogens. Perhaps the most visible example of the kinds of patterns that can be defined by reaction diffusion systems are those seen in animal markings, such as the stripes of the zebra or the spots of the leopard which have also been attributed to reaction diffusion processes (Murray 1981, 1988). Most of the markings on animal skins are for the purpose of camouflage, and therefore those patterns are generally somewhat irregular for that reason. However there are cases where animal and plant markings are intended to attract attention, and in those cases the true potential of morphogenic processes as a representation of geometrical form is demonstrated. This is seen for example in poisonous animals, like the caterpillar shown in figure 3 B, as well as in a variety of poisonous snakes that show periodic geometrical patterns of rings, diamonds, or stripes, as well as in animals that display for mating purposes, like the plumage of a peacock, and of various birds of paradise, and in the plant kingdom it is seen in the forms of flowers. The symmetry and periodicity observed in these examples can be seen as both evidence of the properties of morphogenesis, and at the same time, as properties of biological vision, whose particular sensitivity to periodicity and symmetry are exploited by those morphogenic markings in order to attract visual attention.

In the case of animal coat markings the chemical patterns only define different patterns of coloration. But the same spatial addressing scheme is also responsible for defining the pattern of tissue types in the embryo, for the pattern of concentration of these morphogens during a critical period of development has been shown to be responsible for permanently marking the tissue for subsequent development into bone versus muscle tissue etc. This therefore explains some of the geometrical regularities observed in the shape of the muscles, bones, and internal organs of the body. The periodicity in morphogenesis is ultimately responsible for the periodic segments observed in the bodies of worms and insects, in the vertebrae of vertebrates, and similar resonances have been implicated in many other symmetries and periodicities in plant and animal forms, including the bilateral symmetry of the human body, the pentalateral symmetry of the starfish, the angular and radial periodicity of the bones in the human hand and fingers, and the geometrical forms observed in plant and flower structures. Murray (1988) makes the connection between chemical and vibrational standing waves, showing how a variety of different animal coat patterns can be produced as standing waves in a steel plate cut in the shape of an animal skin, shown in figure 3 C.

Figure 3

A: A periodic banded pattern revealed by chemical staining emerges in a developing embryo, due to a chemical harmonic resonance whose standing waves mark the embryonic tissue for future growth. B: This chemical harmonic resonance has been identified as the mechanism behind the formation of patterns in animal skins, as well as for the periodicity in the vertibrae of vertibrates, the bilateral symmetry of the body plan, as well as the periodicity of the bones in the limbs and fingers. C: Murray shows the connection between chemical and vibrational standing waves by replicating the patterns of leopard spots and zebra stripes in the standing wave resonances in a vibrating steel sheet cut in the form of an animal skin.

7.2 Properties of Harmonic Resonance

There has been much interest recently in the phenomenon known as chaos theory (Gleik 1987) in which spatial or temporal pattern is seen to emerge unexpectedly in otherwise disorganized systems. Chaos theory has even been implicated in theories of neurocomputation (Freeman 1995). However chaos is somewhat of a misnomer, since the phenomenon is better described as unexpected order rather than disorder. Furthermore, many of the phenomena that fall under the rubric of chaos theory, such as period doubling and limit cycles, are actually manifestations of harmonic resonance, an orderly rather than a chaotic organizational principle.

There are several properties of the harmonic resonance model that are suggestive of human recognition. Unlike a rigid template, the pattern defined by a standing wave representation is elastic and adaptive. This can be seen in the manner that the spatial patterns of animal skins are defined. The parameters of the reaction-diffusion that distinguish between the spots and stripes of the tiger, zebra, leopard, and giraffe are encoded as general rules for the generation of those patterns rather than as a spatial template of any one such pattern. For example if a spot or stripe were to be fixed at one point as the pattern was emerging, the rest of the pattern would redistribute itself to adapt to that fixed feature while maintaining the general character of the encoded pattern. This invariance in the representation allows one set of parameters to generate an infinite variety of exemplars of any particular pattern type, or to adapt most flexibly to any fixed constraints or boundary conditions. It is harmonic resonance that explains the adaptiveness of the body plan in morphogenesis to variations in the geometry of the embryonic tissue. This adaptiveness is seen in most dramatic form in the body(ies) of siamese twins, where the body plan is observed to split like a mirror reflection, bifurcating every bone, muscle, tendon, and blood vessel as if it were part of the original plan. This kind of invariance to distortion is a prominent characteristic of human recognition also, as seen for example in the ease with which we recognize wildly distorted caricatures of familiar faces, or the distorted reflections in a curved mirror.

7.3 Emergence in Harmonic Resonance

A soap bubble is the classical physical analogy used in Gestalt theory (Koffka 1935 p. 107, Attneave 1982) to exemplify the principle of emergence. However the standing wave offers an even more dramatic example of the principle of emergence, and the kind of holistic processes identified by Gestalt theory. Like the soap bubble, a standing wave pattern in a flute, for example, is the result of relatively simple local interactions at the molecular level. Yet the effects of these interactions are as global as the resonating system itself. Unlike the soap bubble, the resonance can define a whole set of unique patterns corresponding to the fundamental and its higher harmonics, as seen in the Chladni figures. The emergent patterns defined by those harmonics are not rigid, or template-like, but more like an elastic template that automatically conforms to irregularities in the resonating cavity. For example if a flute is curved, or flared at the end like a trumpet, or bulging in the middle like a barrel, the periodic pattern of the resonance will be correspondingly deformed, defining periodic segments of equal volume, although of unequal geometry. In other words, the resonance defines the topology, rather than the topography of the encoded forms. Resonances in connected systems, such as the engine and chassis of your car, have a natural tendency to synchronize or couple with each other (Dewan 1976, Strogatz & Stewart 1993) so as to produce a single emergent oscillation which exhibits higher harmonics which are characteristic of each component resonator, embedded in a fundamental waveform that captures the resonance of the system as a whole.

7.4 Harmonic Resonance in the Brain

Oscillations and temporal resonances are familiar enough in neural systems and are observed at every scale, from long period circadian rhythms, to the medium period rhythmic movements of limbs, all the way to the very rapid rhythmic spiking of the single cell, or the synchronized spiking of groups of cells. Harmonic resonance is also observed in single-celled organisms like the paramecium in the rhythmic beating of flagella in synchronized travelling waves. Similar waves are observed in multicellular invertebrates, such as the synchronized wave-like swimming movements of the hydra and the jellyfish, whose decentralized nervous systems consist of a distributed network of largely undifferentiated cells. The muscle of the heart provides perhaps the clearest example of synchronized oscillation, for the individual cells of the cardiac muscle are each independent oscillators that pulse at their own rhythm when separated from the rest of the tissue in vitro. However when connected to other cells they synchronize with each other to define a single coupled oscillator. The fact that such unstructured neural architectures can give rise to such structured behavior suggests a level of computational organization below that of the switching and gating functions of the chemical synapse. Vertebrates too exhibit prominent rhythmic motions, most evident in simpler vertebrates such as caterpillars and centipedes, but even larger vertebrates such as snakes, lizards, fish, and eels exhibit a graceful undulating motion suggestive of an underlying wave-like computational mechanism. Strogatz & Stewart (1993) have even characterized the movement of larger mammals in terms of oscillations, showing for example how the various gaits of a horse (trot, canter, gallop, etc.) correspond to the various modes of oscillation of four coupled oscillators. The idea of oscillations in neural systems is not new. However the proposal advanced here is that nature makes use of such natural resonances not only to define rhythmic patterns in space and time, but also to define static spatial patterns in the form of electrical standing waves, for the purpose that is commonly ascribed to spatial receptive fields. While the specific neurophysiological evidence for this pattern formation device remains to be sought out and identified, I will show that as a paradigm for defining spatial pattern, the standing wave offers a great deal more flexibility and adaptiveness to local conditions than the alternative receptive field model, and that a single resonating system can replace a whole array of hard-wired receptive fields in a conventional neural model.

7.5 Physiological and Psychophysical Evidence

The neurophysiological basis for a standing wave theory of neural representation is supported by the observation that blocks of neural tissue that are connected by electrical synapses, or gap junctions, to form a neural syncytium have been shown to exhibit synchronous spiking activity (Kandell & Siegelbaum 1985). Dermietzel & Spray (1993) have identified gap junctions in cortical and subcortical tissue, and show that gap junctions are ubiquitous in the brain and nervous system. Peinado et al. (1993) also implicate gap junctions in local cortical circuits. However harmonic resonance theory does not strictly require gap junctions, for the cell membrane that acts as an insulator for the flow of direct current does not insulate an alternating current (AC) or voltage fluctuations, which are free to pass from cell to cell like an AC current that crosses the insulating dielectric of a capacitor. That is why, for example, it is possible to measure neural activity with extracellular as well as intracellular electrodes. Bremer (1953) observed electrical oscillations in the cat spinal chord, that maintain synchronization from one end of the chord to the other, even when the chord is severed and reconnected by contact alone. Bremer observes that the electrical synchrony along the spinal chord propagates faster than electrical impulses. Gerard & Libet (1940) publish similar observations for the rabbit. In more recent literature a great variety of different kinds of oscillations have been associated with the visual, somatosensory, and motor cortices, suggesting that they may mediate functional integration of sensory or motor information processing in the brain. (Eckhorn et al. 1988, Nicolelis et al. 1995, Murthy & Fetz 1992, Sompolinsky et al. 1990). Hashemiyoon & Chapin (1993, 1994) report retinally derived dark-spontaneous fast frequency oscillations throughout the subcortical visual system of rats which are suppressed by tonic light stimulation. They remain remarkably phase coherent while fluctuating between multiple frequencies approximating 10, 20, and 40 Hz. Gray et al. (1989) report stimulus induced ~40 Hz oscillations in the visual cortex and suggest a functional role for these oscillations in visual processing. Several researchers have proposed that such synchronous oscillations are related to the integration of the conscious experience (von der Malsburg & Schneider 1986, von der Malsburg 1987, Edelman 1987, Llinás 1983, Crick et al. 1990, Singer et al. 1993, Eckhorn et al. 1988, Zeki 1993, Bressler et al. 1993).

7.6 Pattern Recognition by Tuned Resonators

The standing wave and the patterned receptive field share the property that they each define a spatial pattern in the neural substrate. In the conventional neural network paradigm, the cell body acts as the focal point, whose state of electrical activity represents the presence or absence of a corresponding pattern of activation sampled in the cell's receptive field. The standing wave pattern on the other hand appears at first sight to be a more distributed representation, in that the presence of such a pattern in the neural substrate establishes a patterned interaction between the resonating neurons, i.e. the activation of any one cell depends on the total pattern of activation in all neighboring cells, but there is no single cell that is active in the presence of a particular pattern, and inactive in the absence of that pattern, as is the case with the cell body in the neural network paradigm. This focal point is crucial, since it would seem to be the very essence of a recognition system to reduce a complex spatial match to a single match value. There is however a quantity that is associated with each pattern of resonance. In the case of the Chladni figures depicted in Figure 1, each individual pattern is associated with a unique temporal frequency of oscillation, or audible tone. Therefore an audio recording of the vibrating steel plate could be used to uniquely identify which pattern was present on the plate during recording. Furthermore, an audio playback of that frequency in the presence of the plate would have the effect of regenerating that same pattern of resonance back on the original plate. The audio tone can therefore be considered as an abstracted representation, or reduced dimensionality encoding of the spatial pattern on the plate. Therefore matching the tone generated by a vibrating plate to a tone stored in memory corresponds to a recognition of that spatial pattern, just as the activation of a cell body in a receptive field model represents a recognition of the spatial pattern present in its input field. The item in the resonance model corresponding to the cell body in the receptive field model can be envisaged as some kind of tuned resonator, perhaps a cell with a natural tendency to spike at a characteristic frequency.

The principle behind this concept of recognition can be demonstrated using a Chladni plate coupled to an array of acoustical resonators tuned to the specific harmonic frequencies of that plate. Figure 4 A shows three resonators coupled to a Chladni plate, tuned to three selected patterns of standing waves from figure 1. For convenience these will be called the "+", "x", and "/" patterns. When the plate is set into vibration, the standing wave pattern that appears on the plate activates the resonator tuned to that pattern as suggested for each pattern in figure 4 A. The system automatically incorporates reification with recognition, for just as the vibration of the plate with a particular standing wave pattern activates its corresponding resonator, so also does the vibration of the resonator at its characteristic frequency automatically regenerate its characteristic pattern back on the plate, as suggested in figure 4 B.

Figure 4

A: A bank of tuned resonators tuned to the frequency of three specific standing wave patterns are coupled to the plate to behave as feature detectors, that become active whenever their pattern of standing waves is present on the plate. B: The system automatically performs reification with recognition, for the activation of any of the resonators regenerates its characteristic standing wave pattern back on the plate. C: If the plate is resting on rubber ridges in the form of one of the standing wave patterns, the ridges behave as an input pattern, forcing the resonance on the plate to conform to the pattern of the input.

7.7 Input Pattern Applied by Damping

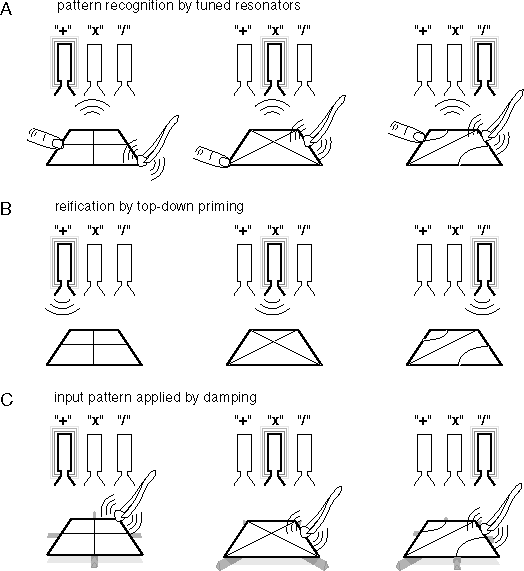
Waller (1961) describes how different patterns of standing waves are produced on a steel plate. In Waller's technique the resonance is energized by a piece of dry ice pressed against the plate, where the gas generated by sublimation of the ice produces a gap between the ice and the plate that opens and closes periodically as the gas escapes. The significant property of this method of energizing the oscillations is that it does not force the oscillations at any particular frequency, but allows the natural resonance of the plate to determine the period of the vibration. A similar principle is seen in musical instruments. For example the sound of a trumpet is energized by the pulsing of the trumpeter's lips. However that pulsing is triggered by the sound waves reflected back from the far end of the trumpet, so the final resonance is determined not by the local dynamics of the lips, as much as by the resonance of the trumpet/lip system as a whole, with every part of the resonant cavity contributing to the final oscillation. Waller describes how higher harmonic patterns are achieved by pressing the dry ice harder against the plate, just as a trumpeter can jump to a higher octave by pursing his lips and blowing harder, which in turn doubles the spatial frequency of the standing wave pattern in the body of the trumpet.The full range of Chladni figures is obtained by damping the plate at various points, either with the touch of a finger or by resting the plate on rubber studs or ridges. The damped points restrict the standing wave patterns to those that exhibit stationary nodes coincident with the damped points. This is the same principle used in a flute, where an open hole damps the vibration of air at that point in the tube, allowing only standing wave patterns to emerge that have a node at the location of the open hole. The pattern of damping can therefore be seen as corresponding to the input pattern in the receptive field model, because the pattern of damping calls up a corresponding pattern of standing waves that matches the pattern of the input, as suggested in figure 4 C, where the plate is shown resting on rubber ridges that match the nodes of the three standing wave patterns corresponding to the three resonators. A non-specific energization of the plate while resting on these ridges therefore calls up the standing wave pattern that matches the pattern of damping, and that standing wave in turn activates the resonator tuned to its characteristic frequency, which represents the recognition of the pattern of damping present on the plate.

7.8 Emergence, Reification, Multistability, and Invariance

There are several significant differences between the receptive field or template model of recognition and that of the Harmonic Resonance model. For the Harmonic Resonance model automatically exhibits the Gestalt properties of emergence, reification, multistability, and invariance, not as specialized circuits or mechanisms contrived to produce those properties, but as natural properties of the resonance itself. Emergence in the Harmonic Resonance model is seen in the fact that there is no need for a set of specialized spatial receptive fields devised to match all of the patterns to which the system is tuned, because the spatial patterning mechanism in harmonic resonance occurs in emergent fashion in the natural vibrational modes of a homogeneous steel plate. This defines a basis set of geometrical patterns in an ascending order of complexity, corresponding to the eigenfunctions of the plate. The tuned resonators which respond to these vibrational modes are very simple devices, which could either be tuned individually to the harmonics of the plate, or they could be devised to adjust their own tuning adaptively to match the temporal frequencies commonly produced by the plate to which they are coupled. Emergence therefore offers a simple mechanism whose dynamic behavior is very much more complex than its architecture would suggest. For the simple plate and resonator system is functionally equivalent to a much more complex neural network model with special patterned receptive fields tuned to detect every pattern to which the system responds. It is the emergent nature of this central mechanism of pattern detection that accounts for the other Gestalt properties of the system i.e. reification, multistability, and invariance.

Reification occurs automatically with no additional mechanism required, for the vibration of the resonator at its characteristic frequency automatically regenerate its characteristic pattern back on the plate. Therefore if a noisy or irregular or incomplete pattern of damping is presented on the plate, the resonance resulting from that input pattern will set up the nearest matching standing wave pattern, which in turn will activate the corresponding resonator. The vibration of that resonator in turn will reify or complete its pattern back on the plate, automatically filling-in any missing features, as suggested in figure 5 A. This property of the Harmonic Resonance model corresponds to the perceptual tendency to perceive complete objects even when portions of them are occluded.

Figure 5

A: In the case of noisy or incomplete input patterns, the system automatically fills-in or completes the missing portions of the pattern, while registering the identity of the recognized pattern in the resonator response. B: In the case of ambiguous patterns the system becomes multi-stable between alternative interpretations. C: Even for simple inputs the system can be multi-stable when stimulated to higher energies, interpreting the input with any standing wave that contains the input as a subset. This excludes the pattern on the right. D: The system is invariant to elastic deformations of the input pattern, as long as the global gestalt is preserved.

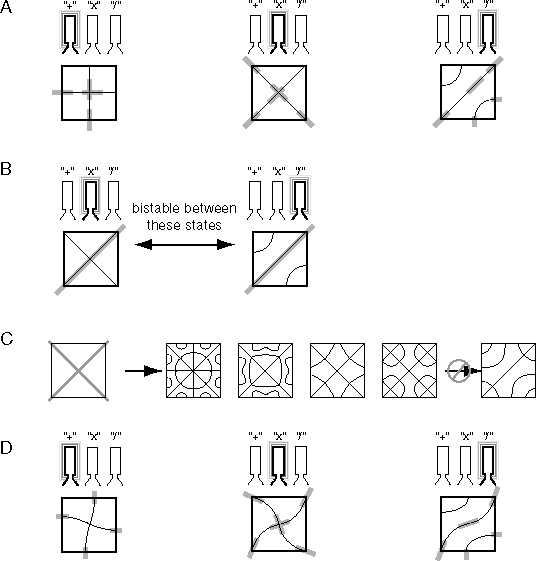
Multistability is also an intrinsic property of the Harmonic Resonance model, which not only makes the model consistent with the properties of perception, but the multistability itself provides interesting functional properties to the recognition system. Figure 5 B depicts a damping input pattern which might be interpreted as either half of an "X" pattern, or the central diagonal of the "/" pattern. In the presence of this input therefore the system becomes bistable between these two standing wave interpretations. The activation of the two resonators will also alternate in synchrony with the alternation of patterns on the plate, i.e. the recognition of the identity of the patterns alternates with the patterns themselves. Any additional evidence present in the input will bias this competition. For example if one of the un-damped corners of the plate is lightly damped with the touch of a fingertip, this will immediately favor the "X"- feature interpretation which is damped along that diagonal, and that tiny bias factor results in the complete "X"-feature pattern being reified on the plate. This is consistent with the observed properties of bistable stimuli such as the Necker cube, in which every portion of the percept appears to invert with the inversion of the spatial interpretation of the stimulus, suggesting a complete inversion of a high-resolution low-level rendition of the perceptual experience, rather than the flipping of a pair of higher-level abstract feature recognition nodes. The Necker cube can also be stabilized in one or the other state by providing tiny gaps in the lines where they cross, suggesting one edge occluding another, and this tiny variation in one small portion of the figure will stabilize the entire perceptual structure.

Multistability has further implications for the properties of harmonic resonance as a recognition system. For in fact the response of the system to a given input is not confined to a single standing wave pattern, but as Waller explains, higher harmonics of that pattern can also be evoked by pressing the dry ice harder against the plate, i.e. driving the system to higher energies, just as a trumpeter jumps to higher octaves by pursing his lips and blowing harder. For example if the plate is damped in the pattern of an "X" as suggested in figure 5 C, the lowest energy standing wave in response to this input would be the one with the "X"-shaped pattern of nodes as described above. However if the plate is excited to higher energy states by pressing the ice harder against the plate, then patterns of higher harmonic standing waves can emerge in response to the same stimulus, including the four patterns depicted to the right in figure 5 C (among others), because all of these patterns share in common the "X" shaped nodal pattern across the diagonals of the square. The standing wave pattern depicted on the far right in figure 5 C on the other hand could not appear in the presence of the "X" shaped input, because that pattern requires the freedom to oscillate along one of the diagonals which are damped by the input pattern. The input pattern therefore does not call up the one and only encoded pattern to which it matches best as in the case of the template model, but rather the system tends to call up any of the many encoded patterns of which the input is a subset. In the presence of the input therefore the system is multi-stable, with the lowest energy state representing the simplest encoded pattern that matches to the input, but with additional energy the system can be made to match more complex patterns to the input, as long as those patterns contain the input pattern as a subset. This kind of system can therefore be made to "search through" its catalog of encoded patterns for any given input, by energizing the oscillations to greater or lesser magnitude, corresponding to pressing the ice harder or softer against the plate. As each pattern is matched against the input, that pattern is reified on the plate in full spatial form, and as that pattern appears on the plate, its corresponding resonator becomes energized, thereby labeling the spatial pattern with the identity encoded by the resonator. The lowest energy patterns are represented by the lower harmonics, which define the simplest or least elaborate patterns. The simplest patterns are the most stable, and therefore are the most likely to be perceived, corresponding to the Gestalt notion of prägnanz, or "Gestalt goodness".

Invariance is also a natural property of a harmonic resonance representation, which is a direct consequence of the emergent nature of the encoding. For the spatial pattern is encoded not as a rigid template, but as a complex dynamic interaction between elements in a continuous resonating system. Recognition is therefore invariant to elastic deformations of the pattern on the plate, as long as they maintain their essential global structure. For example the standing wave patterns shown in figure 5 D subdivide the plate into the same number of regions with equal area as those in figure 5 A, and therefore these resonances will activate the same feature detectors despite the distortion in the pattern. The issue of invariance in recognition is often confused in theoretical discussions with a blindness to variation, i.e. a system is considered invariant to a certain stimulus variation if its response is identical across that variation. However invariance in perception does not have that character, for a pattern that varies for example through rotation, translation, or scale, is recognized as the characteristic pattern, and at the same time it is perceived to be rotated, translated, or scaled. Although the recognition itself is invariant to these transformations, the percept is observed to reflect those stimulus variations. This suggests a two-level response, with invariance at the higher level that is nevertheless coupled to a lower level reified representation in which those variations are plainly evident. This is exactly what occurs in the Harmonic Resonance model, because the pattern completion occurs in the reified representation with respect to the deformations of the pattern as seen in figure 5 D, while the higher level recognition represented by the resonator response remains invariant to those distortions. This unique property of harmonic resonance, so clearly manifest in the subjective experience of vision, is virtually impossible to account for with a neural network model due to the rigid template-like property of the neural receptive field.

7.9 Rotation Invariance in Recognition and Completion

Invariance of an even more impressive form is observed in standing waves generated in a circular symmetric resonator. Figure 6 A (adapted from Waller 1961 pp. 9 and 27) depicts some of the standing wave Chladni figures that can be produced on a circular steel plate clamped at its midpoint, sorted by the number of diameters and concentric circles present in the pattern. (The patterns [0,0] and [0,1] expressed in terms of [diameters, circles] are not actually possible to produce on a steel plate for technical reasons, and are depicted here for theoretical completeness of the representation.) These patterns are shown with one node line oriented vertically. However as a consequence of the symmetry of the plate, these same patterns can actually occur at any orientation, while maintaining the same frequency of vibration. Figure 6 B (adapted from Waller 1961 p. 9) plots the vibration frequency of some of these patterns as a function of the number of diameters in the pattern (corresponding to the columns in figure 6 A), and the number of concentric circles (corresponding to the rows in figure 6 A). The frequencies are expressed as multiples of a fundamental frequency. For example the "X" or "+" shaped pattern [2,0] with two diameters and no circles, has a vibration frequency of 1, whereas the "asterisk" pattern [3,0] has a vibrational frequency between 2 and 3. Waller notes that no two frequencies are exactly equal, and that therefore the frequency uniquely encodes the range of possible patterns. The diagram can be extended indefinitely to greater numbers of diameters and circles, although the higher harmonics require ever increasing energy of vibration.

Figure 6

A: Chladni figures for a circular plate, sorted by the number of [diameters, circles] in each pattern. These patterns can appear at any orientation on the plate. Each distinct pattern has a unique vibration frequency, plotted in B. The vibration frequency therefore offers a rotation invariant representation of the pattern present on the plate.

The rotation invariance relation between the spatial pattern of standing waves and the corresponding vibration frequency is significant. For it means that in the presence of an "input pattern", i.e. a pattern of damping, the plate will resonate at the frequency corresponding to that pattern, and that frequency will remain unchanged as the input pattern is rotated to any angle. A bank of resonators tuned specifically to the fundamental frequencies of vibration of the plate therefore encode a rotation invariant representation of those patterns. The unique property of harmonic resonance is in the coupling between the frequency and its pattern. For if a resonator is activated top-down, i.e. in the absence of any input stimulus, the activation of that resonator in the vicinity of the plate will tend to regenerate its corresponding pattern on the plate. If the resonator is activated at a lower amplitude in the absence of any input stimulus, this will result in an indeterminate pattern on the plate, since the pattern is attempting to reify itself at all orientations simultaneously, as suggested in figure 7 A. However if the top-down activation of the resonator is applied at sufficiently high amplitude, the pattern will emerge on the plate at a random orientation, and since the orientation of the emergent pattern is unconstrained by the top-down signal, the reified pattern will be free to spin on the plate like a compass needle as suggested in figure 7 B.

Figure 7

Reification through rotation invariance. A: With a weak top-down priming of a "+" feature, the reification is indeterminate, as the pattern attempts to reify itself at all orientations simultaneously. B: With a stronger prime the pattern is reified at some arbitrary orientation, but remains free to spin like a compass needle. C: A touch on the plate with a finger breaks the symmetry and locks the reified pattern to an orientation that matches the damped point. D: A noisy pattern is reified and completed at the orientation that best matches the primed pattern.

In the presence of a weak or partial input applied simultaneously to a moderate top-down prime, the input will anchor the orientation of the pattern projected top-down, resulting in a bottom-up / top-down resonance, in which the input pattern is interpreted and filled-in in the context of the current top-down prime. For example a top-down priming of the circular plate with an "X"-feature oscillation could potentially regenerate that "X" pattern at any orientation. A touch of a finger on the rim of the plate during this priming would fix that "X" pattern at an orientation where one node line coincides with the damped point, as suggested in figure 7 C. The standing wave model also mirrors several properties of recognition in the bottom-up mode. In the absence of a top-down priming signal, a noisy or ambiguous input pattern will stimulate the appearance of the nearest matching pattern encoded in the harmonic representation, and that best matching pattern will be reified on the plate, with any missing details filled-in, as suggested in figure 7 D. It is this property of bottom-up top-down matching across an invariance relation that represent the greatest promise of the Harmonic Resonance theory as a representation of perceptual processes, for it now provides a mechanism for the invariance observed in perception.

7.10 Dynamic Pattern Formation

One of the most compelling features of a harmonic resonance representation is that the same mechanism that defines static patterns of standing waves is also capable of generating complex dynamic patterns of the sort that are most likely responsible for the sinusoidal oscillations in fish and snakes, and the periodic cyclic pattern of motion of the centipede's feet. For such complex patterns can be generated by interference between spatial waves driven at slightly different frequencies, resulting in a cyclic rotation of the standing wave pattern at a rate that is proportional to the frequency difference between the component waveforms. In other words the orientation and rate of rotation of a spatial standing wave pattern can be controlled by the phase shift between component driving oscillations, in the manner of the rotating Lissajou figures on an oscilloscope, generated by plotting two sinusoids against each other in x and y axes on the scope. As with the Lissajou figures, complex dynamic figures can be generated by addition of more component waveforms which can result in endless combinations from a small set of pattern primitives.

7.11 Harmonic Resonance and Binding

The Harmonic Resonance theory finally provides a promising computational principle to account for the unity of the conscious experience, for it is in the very nature of resonances in different resonators to unite when the resonators are coupled, to produce a single coherent coupled oscillation of the system as a whole. The individual oscillators that make up the coupled system have a mutual influence on each other, each one inducing the others to match to its own oscillation, resulting in a single coherent global oscillation state, as described by Dewan (1976) and by Strogatz & Stewart (1993).

When the oscillators which are being coupled are in the form of spatial resonators, like a Chladni plate, the coupling between different plates will not only bind them in synchronous oscillation, but that synchrony in turn will generate similar patterns on the coupled plates. The spatial resonator in effect transforms the spatial pattern of its standing wave into a highly structured, but one-dimensional temporal waveform, which is communicated to the other resonators through the coupling. The other resonators in turn transform that temporal signal back into a spatial pattern defined by standing waves. But the influence is reciprocal through the coupling, so the resonance in the other plates also get communicated back to the first, locking the spatial patterns on the coupled plates to each other. If the perceptual information in different cortical maps is expressed in terms of standing wave patterns, the coupling between these maps would synchronize the spatial patterns within them like the pictures on an array of television sets in a shop display which are all tuned to the same channel, except that the synchrony of the cortical maps is not due to the fact that they are all presenting identical copies of the same signal, but because each contributes its own influence to a pattern of resonance that is shared in common among those maps.

It is also in the nature of harmonic resonance to form multiple identical or similar copies of a particular waveform, replicated in mirror-reversed symmetry, as seen in many of the patterns in figure 1. For a pattern which is symmetrical about a diagonal, for example, the patterns of resonance on opposite sides of the diagonal can be considered as two separate copies of the same resonant half-pattern that are coupled to each other in a single resonance. Neurophysiological mapping of the somatosensory cortex, which was originally thought to define a simple somatotopic map, has on closer examination revealed multiple copies of the body map often in mirror-reversed patterns (Kolb & Whishaw 1980, p. 176) suggestive of a standing wave representation. Now identical copies of a cortical map are not very useful. However if the dynamic properties of the resonating substrate were slightly different in different cortical regions, specialized dynamic properties of each different cortical area would enhance or emphasize specific aspects of the resonance in those areas, while maintaining a dynamic coupling to other areas with slightly different dynamic properties. However the special features enhanced in one brain area would not remain isolated to that area, but rather the effects of any resonance in any brain area would immediately modulate the resonance in all other areas simultaneously, as seen in the phenomenon of audio filtering, as when various acoustical cavities are coupled to each other. This principle is also observed in analog RF circuits, where the addition of different components at different points in the circuit does not process the signal in an input-output manner "downstream" of the added component as in digital circuitry, but rather it modulates the signal in the circuit as a whole, enhancing certain aspects of the waveform in all of the components of the circuit simultaneously, although the exact waveform observed within each component exhibits subtle variations.

8 Conclusion

The harmonic resonance theory is not a fully specified theory of neurocomputation, but a paradigm, i.e. a set of assumptions as to the fundamental principles behind biological computation, as a challenge to the more conventional concept of neurocomputation embodied in the neuron doctrine. Whether or not this principle is actually operational in the brain is a subject for future investigation, and for re-examination of existing data in the light of the new hypothesis. In fact there may already be considerable evidence available to other researchers which might either support or refute the hypothesis, but that evidence remains unpublished because its significance is only revealed in the light of the new hypothesis. It is for this reason that every paradigmatic hypothesis deserves at the very least to be exposed to the larger community, as long as it can be shown to be truly unique and original, and not easily refuted by trivial arguments.

A great deal of work remains to be done before the harmonic resonance theory can be considered a real neurophysiological theory that makes testable predictions. In the first place the model will have to be specified in greater detail, to define the specific representational code of visual neurons, which can be matched against actual neurophysiological recordings. For the harmonic resonance theory suggests that the significant signal in the brain is not carried by the powerful spikes of the action potential, but by a more subtle and pervasive graded potential oscillation, as recorded by Pribram (1971) and Bland et al. (1978). The theory will have to be elaborated to identify exactly which systems or circuits are resonating in the brain, how those resonances are sustained, how they are modulated by sensory input, and how the subjective variables of perceived color, shape, and form are encoded in the standing wave representation. The harmonic resonance theory will also have to explain why certain cortical neurons seem to behave as if they were feature detectors, and to provide an alternative functional explanation for that observed behavior.

Even as a paradigmatic hypothesis, the presentation of the principles of harmonic resonance in this paper might seem unsatisfactory to scientists accustomed to a more rigorous mathematical specification of the functional principles of a proposed model. However there are certain classes of physical systems which simply do not succumb to mathematical analysis because the phenomena in question are already the simplest model of themselves, i.e. there is no way to reduce the phenomena to simpler mathematical terms without setting prohibitively restrictive constraints on the parameters of the system. In all but the simplest cases, harmonic resonance has exactly this property. And it is that very property that represents the most interesting aspects of harmonic resonance as a representation in the brain. Chladni (1787) and Waller (1961) both reference work by various authors who provide mathematical solutions to the equilibrium states of various standing wave patterns found on steel plates. But these analyses are an abstraction or reductionist description of the actual mechanism of harmonic resonance, which is actually a fine-grained process involving molecular interactions throughout the resonating system resulting in global effects. The mathematical solutions for steel plates have only been developed to account for the simplest of these patterns, like those for a circular or square plate. This kind of analysis becomes intractable in the case of irregular or arbitrary shaped steel plates, or plates of non-uniform thickness. And yet it is this very flexibility that represents the most interesting aspect of the resonance. If the discussion were limited to the simple cases for which analytical solutions have been found, the theory would degenerate to a template theory, and thereby lose its most appealing properties.

Physical systems that defy mathematical characterization are often addressed numerically, using computer simulations. This is the approach used for example to model the behavior of the atmosphere, which is approximated by quantization of the system in space and time to tiny local elements which are simple enough to be treated as a single point. However this approach too has its limits, for the quantization in space and time inevitably introduces inhomogeneities into the system. The case of harmonic resonance is even more problematic for numerical simulations than a model of the atmosphere, because atmospheric parameters such as temperature, pressure, and humidity tend to diffuse isotropically into adjacent regions in a relatively simple manner, so that these parameters can be computed fairly accurately by considering only nearest neighboring regions. In the case of standing wave pattern in a resonating system on the other hand, the local value of the pattern depends on the configuration of the entire resonating system as a whole, and cannot be even approximated from the values of adjacent regions of the system, for resonance does not simply diffuse between adjacent points in the system, but is influenced by the entire configuration of the system as a whole, as evidenced by the fact that a touch of the plate at any point will completely change the standing wave pattern across the whole plate.

The very fact that harmonic resonance exhibits this Gestalt-like nature, and the fact that these kinds of systems are so difficult to characterize both mathematically and computationally, provides all the more reason to investigate these phenomena as a possible property of biological computation, to account for exactly those aspects of perception which have defied characterization in more rigorous analytical terms. If this work must be done "by analogy" using vibrating steel plates, that does not in any way invalidate the results, for the vibrating steel plate is itself a computational mechanism, albeit one whose operational principles are radically different from any known computational device, and therefore the "output" of the steel plate is no different in principle from the output of a computer simulation, as long as the same phenomena can be replicated by different investigators. The fact that resonance exhibits similar properties whether expressed as a physical, electrical, chemical, or acoustic resonance shows that resonance is a general principle that transcends any particular physical instantiation, and thereby represents a higher order organizational principle of physical matter. Considered as a computational paradigm, harmonic resonance has unique emergent properties that cannot be meaningfully reduced to an equivalent Turing machine description. The message of Gestalt theory is that it is exactly this kind of unconventional enigmatic physical phenomenon which should be sought out as the functional principle behind biological computation.

Finally, the harmonic resonance theory also offers an explanation for one of the most enduring mysteries of human experience, which is the question of why resonances in musical instruments and the rhythmic beating of drums have such a powerful ability to evoke the deepest emotional response in the human soul. I propose that the musical instrument represents man's first modest success at replicating the physical principle behind biological computation, and the strong emotional response evoked by these inanimate resonances reflects an unconscious recognition of the essential affinity between mind and music.

References

Attneave F. (1971) "Multistability in Perception" Scientific American 225 142-151

Attneave F. (1982) "Prägnanz and soap bubble systems: a theoretical exploration" in Organization and Representation in Perception, J. Beck (Ed.), Hillsdale NJ, Erlbaum.

Ballard D. H. & Brown C. M. (1982) "Computer Vision". Prentice-Hall, Englewood Cliffs, NJ.

Barlow H. B. (1972) Single Neurons and Sensation: A neuron doctrine for perceptual psychology. Perception. Perception 1, 371-394.

Barlow H. B. (1995) The Neuron Doctrine in Perception. In M. Gazzaniga (Ed.), The Cognitive Neurosciences. Cambridge: MIT Press.

Barrett T. W. (1969) The Cortex as Interferometer: The transmission of amplitude, frequency, and phase in cortical structures. Neuropsychologica 7, 135-148.

Biederman I. (1987) "Recognition-by-Components: A Theory of Human Image Understanding". Psychological Review 94 115-147

Bland B. H., Anderson P., Ganes T., & Sveen O. (1978) Automated Analysis of Rhythmicity of Physiologically Identified Hippocampal Formation Neurons. Experimental Brain Research 38, 205-219.

Bremer F. (1953) "Some Problems in Neurophysiology". London: Athlone Press.

Bressler S., Coppola R., & Nakamura R. (1993) Episodic Multi-Regional Cortical Coherence at Multiple Frequencies During Visual Task Performance. Nature 366: 153-156.

Carpenter G. A. & Grossberg S. (1987) A Massively Parallel Architecture for a Self-Organizing Neural Pattern Recognition Machine. Computer Vision, Graphics, and Image Processing 37, 54-115.

Chladni, E. E. F. (1787) "Entdeckungen über die Theorie des Klanges". Leipzig: Breitkopf und Härtel.

Crick . H. & Koch C. (1990) Towards a Neurobiological Theory of Consciousness. Seminars in the Neurosciences 2: 263-275.

Cristiansen B., Alstrøm, & Levinsen M. T. (1992) Ordered Capillary-Wave States: Quasicrystals, Hexagons, and Radial Waves. Physical Review Letters 68 (14) 2157-2160.

Damasio A. (1989) Time-Locked Multiregional Retroactivation: A Systems-level Proposal for the Neural Substrates of Recall and Recognition. Cognition 33, 25-62.

Dermietzel R. & Spray D. C. (1993) "Gap Junctions in the Brain: where, what type, how many, and why?" TINS 16 (5) 186-191.

De Valois K. K., De Valois R. L., Yund W. W. (1979) Responses of Striate Cortex Cells to Grating and Checkerboard Patterns. Journal of Physiology 291, 483-505.

De Valois R. L., De Valois K. K. (1988) Spatial Vision (Oxford Psychology Series No. 14) New York: Oxford University Press.

Dewan E. M. (1976) Consciousness as an Emergent Causal Agent in the context of Control Systems Theory. In: G. Globus (Ed.) Consciousness and the Brain: A Scientific and Philosophical Inquiry. New York: Plenum Press, 181-198.

Eckhorn R., Bauer R., Jordan W., Brosch M., Kruse W., Munk M., Reitboeck J. (1988) "Coherent Oscillations: A Mechanism of Feature Linking in the Visual Cortex?" Biol. Cybern. 60 121-130.

Edelman G. (1987) Neural Darwinism: The Theory of Neuronal Group Selection. New York: Basic Books.

Ehrenfels C. Von (1890) Über Gestaltqualitäten. Vierteljaheresschrift für wissenschaftliche Philosophie, 14, 249-292.

Engel A. K., König P., Gray C. M., & Singer W. (1990) Stimulus-Dependent Neuronal Oscillations in Cat Visual Cortex: Inter-columnar Interaction as Determined by Cross-Correlation Analysis. European Journal of Neuroscience 2, 588-606.

Engel A. K., König P., Kreiter A. K., & Singer W. (1991a) Interhemispheric Synchronization of Oscillatory Neuronal Responses in Cat Visual Cortex. Science 252, 1177-1179.

Engel A. K., Kreiter A. K., König P., & Singer W. (1991b) Synchronization of Oscillatory Neuronal Responses between Striate and Extrastriate Visual Cortical Areas of the Cat. Proceedings of the National Academy of Sciences USA 88, 6048-6052.

Faraday M. (1831) On a Peculiar Class of Acoustical Figures and on the Form of Fluids Vibrating on Elastic Surfaces. Phil. Trans. R. Soc. Lond. 225, 563-576.

Freeman W. (1995) Societies of Brains. Hillsdale N. J. Erlbaum.

Fukushima K. (1987) Neural Network Model for Selective Attention in Visual Pattern Recognition and Associative Recall. Applied Optics 26 (23) 4985-4992.

Geissler H.-G. (1997) "Is there a way from behavior to non-linear brain dynamics? On quantal periods in cognition and the place of alpha in brain resonances". International Journal of Psychophysiology 26, 381-393.

Geissler H.-G. (1987) "The temporal architecture of central information processing: Evidence for a tentative time-quantum model". Psychological Research, 49, 99-106.

Geissler H.-G. (1998) "Ultra-precise quantal timing: Evidence from simultaneity thresholds in long-range apparent movement". Submitted Perception & Psychophysics.

Gerard, R. W. & Libet B. (1940) "The Control of Normal and `Convulsive' Brain Potentials". Amer. J. Psychiat., 96, 1125-1153.

Gilbert S. F. (1988) "Developmental Biology" Sunderland MA: Sinauer Associates.

Gleik J. (1987) Chaos: Making a New Science. New York: Penguin Books.

Gray, C.M., Engel, K.A. Koenig, P., & Singer, W. (1990) Stimulus-Dependent Neuronal Oscillations in Cat Visual Cortex: Receptive field properties and feature dependence. European Journal of Neuroscience 2, 607-619.

Gray, C.M., Engel, K.A. Koenig, P., & Singer, W. (1992) Synchronization of Oscillatory Neuronal Responses in Cat Striate Cortex: Temporal Properties. Visual Neuroscience 8, 337-347.

Gray, C.M., Koenig, P., Engel, K.A. & Singer, W. (1989) Oscillatory responses in cat visual cortex exhibit intercolumnar synchronisation which reflects global stimulus properties. Nature 338: 334-337.

Gray, C.M. & Singer, W. (1989) Stimulus-Specific Neuronal Oscillations in Orientation Columns of Cat Visual Cortex. Proceedings of the National Academy of Science USA. 86, 1698-1702.

Grossberg, Stephen, & Mingolla, Ennio (1985). Neural Dynamics of Form Perception: Boundary Completion, Illusory Figures, and Neon Color Spreading. Psychological Review, 92, 173-211.

Grossberg, Stephen, & Mingolla, Ennio (1987). Neural Dynamics of Surface Perception: Boundary Webs, Illuminants, and Shape-from-Shading.. Computer Vision, Graphics and Image Processing, 37, 116-165.

Harrison S. (1989) A New Visualization on the Mind-Brain Problem: Naive Realism Transcended. In J. Smythies & J. Beloff (Eds.) The Case for Dualism. Charlottesville: University of Virginia.

Hashemiyoon R. & Chapin J. (1993) "Retinally derived fast oscillations coding for global stimulus properties synchronise multiple visual system structures". Soc. Neurosci. Abstr. 19 528.

Hashemiyoon R. & Chapin J. (1994) "Retinally derived fast oscillations coding for global stimulus properties synchronise multiple visual system structures". Assoc. Res. Vis. and Ophthal. Abstr. 35 1976.

Hodgkin A. L. & Huxley A. F. (1939) Action Potentials Recorded from Inside Nerve Fiber. Nature 144 710-711.

Hubel D. H. (1988) Eye, Brain, and Vision. New York: Scientific American Library.

Idesawa M. 1991 "Perception of Illusory Solid Object with Binocular Viewing". Proceedings IJCNN

Kandell, E. R., & Siegelbaum, S. (1985) "Principles Underlying Electrical and Chemical Synaptic Transmission".. In Principles of Neural Science, Kandell, Eric R., & Schwartz James H. (Eds.) Elsevier Science Publishing Co., New York.

Kanizsa G, (1979) "Organization in Vision" New York, Praeger.

Kauffman S. A., Shymko R. M., & Trabert K. (1978) "Control of Sequential Compartment Formation in Drosophila". Science 199, 259-270.

Koffka K, (1935) "Principles of Gestalt Psychology" New York, Harcourt Brace & Co.

Köhler, W. & Held R. (1947) The Cortical Correlate of Pattern Vision. Science 110: 414-419.

Kolb B. & Whishaw I. Q. (1980) Fundamentals of Human Neurophsycology, 2nd edition. New York: W. H. Freeman.

Kristofferson A. B. (1990) "Timing mechanisms and the threshold for duration". In: H.-G. Geissler (Ed.), Psychophysical Explorations of Mental Structures, in collaboration with M. H. Müller & W. Prinz. Toronto, Hogrefe & Huber, 269-277.

Kudrolli A. & Gollub J. P. (1996) Patterns of Spatiotemporal Chaos in Parametrically orced Surface Waves: A Systematic Survey at Large Aspect Ratio. Physica D 97, 133-154.

Kudrolli A., Pier B., & Gollub J. P. (1998) Superlattice Patterns in Surface Waves. Physica D 123, 99-111.

Kuhn T. S. (1970) The Structure of Scientific Revolutions. Chicago: Chicago University Press.

Kumar K. & Bajaj K. M. S. (1995) Competing Patterns in the Faraday Experiment. Physical Review E, 52 (5) R4606-R4609.

Lashley K. S. (1942) The Problem of Cerebral Organization in Vision. Biol. Simp., 7, 301-322.